Unterscheidet man die Zahlen des Pascalschen Dreiecks danach, ob sie ohne Rest teilbar sind, ergeben sich interessante Muster.
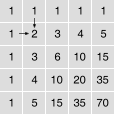Um Handhabung
und Darstellung zu vereinfachen, sind die Zahlen in einem
rechteckigen Raster angeordnet. So ergibt sich ein rautenförmiger
Ausschnitt aus einem um 45° nach links gedrehten Pascalschen
Dreieck.
Alle Zahlen der Spalte ganz links und der obersten Zeile sind gleich 1. Für jede andere Zahl des Rasters addiert man jeweils die Werte des oberen und linken Nachbarn. Die Abbildung oben soll dies veranschaulichen.
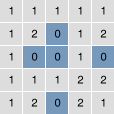In der nebenstehenden Abbildung wurde für alle Zahlen der Rest aus der
Division mit 3 ermittelt. Man kann nun ein Bild erzeugen indem man für
Werte gleich 0 beispielsweise ein blaues Quadrat zeichnet und für Werte
größer 0 ein graues.
Das Pascalsche Dreieck erzeugt schnell sehr große Zahlen. Für die Verarbeitung der Zahlen steht aber nur begrenzt Speicherplatz zur Verfügung. Damit die Zahlen gar nicht erst anwachsen, packt man Addition und Modulo-Operation in eine Schleife. Codefragment in Java:
for (int y = 0; y < zahlen.length; y++) {
for (int x = 0; x < zahlen[0].length; x++) {
if (x == 0 || y == 0) {
zahlen[y][x] = 1;
}
else {
zahlen[y][x] = (zahlen[y][x-1] +
zahlen[y-1][x]) % teiler;
}
}
}Auch mit Excel oder OpenOffice lassen sich Grafiken erzeugen.
Das Pascalsche Dreieck im World-Wide-Web:
de.wikipedia.org/wiki/Pascalsches_Dreieck
site2004.de/raster/pascal.html